Bearing Life Calculator using Equivalent Radial Load
* For Reference Only *
Tool created by APT Bearing, Inc. | Copyright © 2024 APT Bearing Inc. | All rights reserved
Disclaimer:
1. This tool is for demonstration purposes only. It should not be used to calculate life for critical applications. It utilizes estimated load ratings and estimated product specifications to provide estimated bearing life. APT Bearing Inc. uses more sophisticated software to analyze the complete bearing system - multiple bearing rows, radial, axial, moment loads, and actual internal geometry. For assistance, please contact us about your application.
2. This calculation was derived using industry standards as well as assumptions provided by the user.
3. This calculation was derived using Charts and Formulas presented in Rolling Bearing Analysis (4th Edition), by Tedric A. Harris, pg. 722.
4. This tool is for reference only. APT Bearing Inc. is not responsible for errors resulting from data in this tool.
Basic Bearing Fatigue Life
L10= (Cr/P)3 X 106 (Revolution)
L10h = 16667 / n · (Cr/P)3 (hours)
Where:
L10 = Basic rating life
Cr = Basic dynamic load rating (N)
n = R.P.M. (revolutions per minute)
L10h = Basic rating life in operating hours
P = Equivalent load (N)
The basic fatigue life of a rotating deep-groove ball bearing is given as:
General Fatigue Life Correction Factors
The L10 preload life of a bearing is normally adjusted as follows, according to real-world operating conditions:
| Lna | = | a1a2 L10 | where: | Lna = adjusted bearing fatigue life |
a1 = Life correction factor for material and desired statistical reliability, the values for a1 being given below:
Values for Life Correction Factor a1
| MATERIAL | STATISTICAL RELIABLITY (%) | |||||
| 90 | 95 | 96 | 97 | 98 | 99 | |
| Chrome: 52100 | 1.00 | .62 | .53 | .44 | .33 | .21 |
| Stainless: 440 | .50 | .31 | .27 | .22 | .17 | .11 |
a2 = Life correction factor for operating conditions. It has been empirically determined to have a value between 2.0 under ideal operating conditions and 0.2 where one or more of the following conditions may apply:
- The lubricant film thickness between the raceways and the rolling elements is low
- Bearing raceways are excessively misaligned Oscillatory motion
- Rotation speed of the bearing elements is very low
- Contamination or water is present in the bearing
Because there are many factors that determine the bearing life, the above figures should be used conservatively.
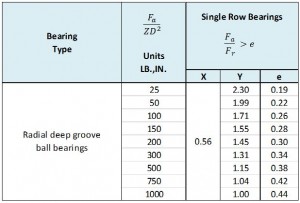
Equivalent Radial Load
In order to calculate an estimated life for a bearing you will need to use the Bearing Lifetime formula listed above. If your application involved purely a radial load applied to the bearing (no axial loading), then you can use the pure radial load to calculate the estimated bearing lifetime. In many situations, the application involves a combination of axial and radial loads. In these situations you may use the formulas and table below to combine the axial and radial loads into an Equivalent Radial Load that can be used in the bearing lifetime formula to calculate an estimated bearing life.
- Pr = Fr
- Pr = XFr +Yfa
When Fa/Fr < e, formula (a) is used. Otherwise formula (b) is used.
Nomenclature is as follows:
Pr = Equivalent Radial Load
V = rotation factor
X = radial factor
Y = thrust factor
Fr = radial load
Fa = thrust load
Z = number of balls
D = ball diameter in inches
When Fa/Fr < e, formula (a) is used. Otherwise formula (b) is used.